Freie Universität Berlin'den matematikçiler, yakın zamanda yaptıkları bir çalışmada, düzlemsel döşeme veya mozaiklemenin, sadece güzel bir desen oluşturmanın ötesinde bir anlamı olduğunu ortaya koydu. Boşluk ve örtüşme olmadan bir veya daha fazla geometrik şekilden oluşan bir yüzeyden oluşan mozaiklemeler, karmaşık matematik problemlerini çözmek için hassas bir araç olarak da kullanılabilir.
Bu, Heinrich Begehr ve Dajiang Wang tarafından kaleme alınan ve yakın zamanda Applicable Analysis adlı bilimsel dergide yayınlanan "Matematikte/Matematikte Güzellik: Mozaikler ve Formülleri" adlı çalışmanın temel bulgularından biridir. Çalışma, karmaşık analiz, kısmi diferansiyel denklemler teorisi ve geometrik fonksiyon teorisi alanlarından elde edilen sonuçları bir araya getirmektedir.
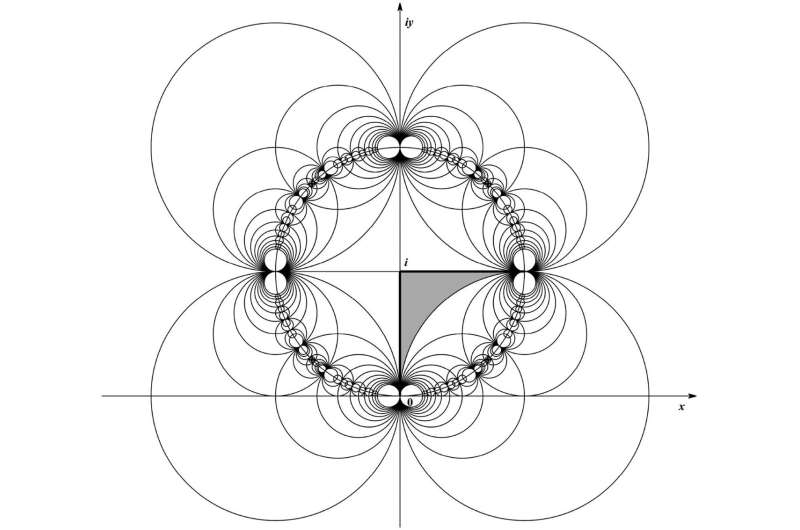
Çalışmanın odak noktası "parkeleme-yansıma ilkesi"dir. Bu ilke, geometrik şekillerin kenarları boyunca tekrarlanan yansımalarının bir düzlemi döşemek için kullanılması ve bunun sonucunda oldukça simetrik desenlerin elde edilmesi anlamına gelir. Düzlemsel mozaiklerin estetik örnekleri M.C. Escher'in çalışmalarında görülebilir. Görsel çekiciliğinin yanı sıra, ilkenin matematiksel analizde de uygulamaları vardır; örneğin, Dirichlet problemi veya Neumann problemi gibi klasik sınır değer problemlerinin çözümünde bir temel gibi.
Profesör Begehr, “Araştırmalarımız, matematiğin güzelliğinin sadece estetik bir kavram değil, aynı zamanda yapısal derinlik ve verimlilik içeren bir şey olduğunu gösteriyor” diyor. "Daha önceki mozaik araştırmaları, şekillerin bir yüzeyi döşemek veya kaplamak için nasıl kullanılabileceğine odaklanmıştı. Örneğin, Nobel Ödülü sahibi Sir Roger Penrose tarafından yürütülen bazı tanınmış çalışmalar. Ancak, parke yansıma yöntemini kullanarak yeni mozaikler oluşturmak, yeni olanaklar sunuyor.
Bu, bu döşeme bölgelerinde fonksiyonları temsil etme yöntemleri geliştirmek için pratik bir araçtır ve matematiksel fizik ve mühendislik gibi alanlarda yararlı olabilir."
Özellikle, fizik ve mühendislikte sınır değer problemlerini çözmek için kullanılabilecek araçlardan bazıları olan Green, Neumann ve Schwarz çekirdekleri dahil olmak üzere çekirdek fonksiyonları için belirli formüller türetmek için kullanılabilir. Bu nedenle, bu çalışma geometrik sezgi ile analitik hassasiyet arasında zarif bir bağlantı kurmaktadır.
Parqueting-reflection ilkesi, on yıldan fazla bir süredir ün kazanmaktadır ve özellikle kariyerinin başındaki akademisyenler arasında bir araştırma konusu olarak popülerdir. İlk geliştirilmesinden bu yana, Freie Universität'te toplam on beş tez ve bitirme projesi bu konuyu araştırmış, ayrıca yurtdışındaki araştırmacılar tarafından yedi tez daha yazılmıştır.
Dikkat çekici bir şekilde, bu ilke sadece Öklid uzayında değil, aynı zamanda hiperbolik geometrilerde de geçerlidir — teorik fizikte ve uzay-zamanın modern görselleştirmelerinde kullanılan türlerde. Bu ilkeye olan ilgi hala yüksektir. Geçen yıl Begehr, Complex Variables and Elliptic Equations dergisinde “Hiperbolik Mozaikleme: Hiperbolik Geometride Schweikart Üçgeni için Harmonik Green Fonksiyonu” başlıklı bir makale yayınladı ve bu makalede, hiperbolik düzlemde Schweikart üçgeni için harmonik Green fonksiyonunu oluşturmak için parke yansıma ilkesinin kullanımını gösterdi.
Wang, “Sonuçlarımızın sadece saf matematik ve matematiksel fizikte yankı bulmasını değil, mimari veya bilgisayar grafikleri gibi alanlarda da ilham kaynağı olmasını umuyoruz” diyor.
Berlin'deki döşeme geleneği
Neredeyse yirmi yıldır, Freie Universität Berlin Matematik Enstitüsü'nde Begehr'in liderliğindeki araştırma grubu, Berlinli matematikçi Hermann Amandus Schwarz (1843–1921) tarafından geliştirilen birleşik yansıma ilkesine dayanan “Berlin ayna döşemeleri” olarak bilinen yöntemi incelemektedir.
Bu yaklaşımda, kenarları düz çizgiler ve dairesel yaylardan oluşan bir dairesel çokgen, tüm düzlem kesintisiz ve tamamen döşenene kadar, üst üste binme veya boşluk kalmayacak şekilde tekrar tekrar yansıtılır. Bu desenler sadece görsel olarak çarpıcı olmakla kalmaz, aynı zamanda fonksiyonların açık integral temsilini de mümkün kılar — bu da karmaşık sınır değer problemlerini çözmek için önemli bir araçtır.
Begehr, “Matematikçiler eskiden sonsuz bir görüntü dizisi oluşturmak için üç parçalı bir makyaj aynası kullanmak zorundaydı” diyor. “Günümüzde, aynı etkiyi elde etmek için yinelemeli bilgisayar programları kullanabiliriz ve bunu karmaşık analizde kullanılan kesin matematiksel formüllerle tamamlayabiliriz.”
Schweikart üçgenleri ve hiperbolik güzellik
Estetik açıdan çok etkileyici olmalarına rağmen, hiperbolik uzaylardaki mozaikler (örneğin dairesel bir disk içindeki mozaikler) matematikçiler için özel bir zorluk teşkil eder. İşte burada “Schweikart üçgenleri” devreye girer: amatör matematikçi ve hukuk profesörü Ferdinand Kurt Schweikart'ın (1780–1857) adını taşıyan, bir dik açı ve iki sıfır açı içeren özel üçgenler.
Bu üçgenler, dairesel bir diskin tam ve düzenli bir şekilde döşenmesini sağlar ve bilgisayar grafik sanatçıları ve mimarlar için yeni ilham kaynağı olan estetik açıdan çekici desenler oluşturur. Aynı zamanda, temel matematiksel yapılar oldukça karmaşıktır ve gelişmiş analitik yöntemler gerektirir.
Görsel bir bilim olarak matematik
Ekibin bulguları, matematiğin genellikle göz ardı edilen bir yönünü vurgulamaktadır: matematik sadece soyut bir disiplin değil, aynı zamanda yapı, simetri ve estetiğin merkezi bir rol oynadığı görsel bir bilimdir. Modern görselleştirme teknikleri, grafik yazılımları ve dijital araçlarla birleştirildiğinde, bu bilgiler daha da anlamlı hale gelir.
Daha fazla bilgi: H. Begehr et al, Beauty in/of mathematics: tessellations and their formulas, Applicable Analysis (2025). DOI: 10.1080/00036811.2025.2510472.